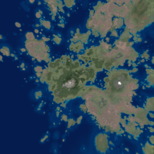
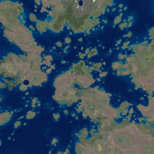
Procedural Generation of Earth-like Planets

Use arrow keys to navigate slideshow, and press F11 for fullscreen

Output:

six images for use as cube map

six images representing normal map

		.
.	.	.	.	.	.	.	.

Data Representation

Sphere is represented as 6 square arrays of 3d vectors

Imagine a cube overinflated until it is a sphere.

Each element in the array contains a 3d vector that represents the terrain elevation at a particular point on the sphere.

Recursively add "bumps"

Start with sphere represented by 6 square arrays of normalized vectors

Choose radius and location for bump (Marsaglia 1972 rejection method)

Use 0.5 + 0.5 * cosine(x) as bump profile, where x is distance from bump center scaled into range 0 - Pi

vector lengths representing elevation are adjusted to make the bumps

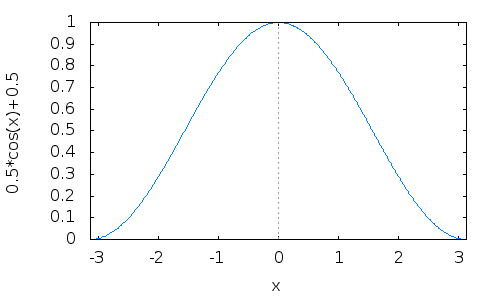
0.5 + 0.5 * cos(x) in the range of -Pi to Pi

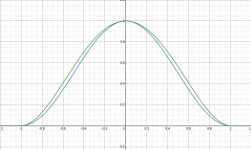
Wed Aug 11 20:14:17 EDT 2021 Note: KdotJPG informs me of a more efficient polynomial that involves no sqrt() or trig functions which produces nearly the same curve:

• s = min(x^2, 1.0);
• (1 - s)^2

Here's a graph, the green line is (1 - s)^2, the blue line is 0.5 + 0.5 * cos(sqrt(s) * PI).

Bumps are recursively added

Each bump has smaller "sub-bumps" distributed around it, likely overlapping

The "sub-bumps" have sub-sub-bumps, and so on.

Modulate bumps with real terrain data...

Modulate bumps with real terrain data...

Each bump has a vector defining its position on the surface of the sphere

Compute quaternion to rotate bump to "front and center"

For each point within the "bump", apply this quaternion

Then the (x,y) components can be used directly (after scaling and offsetting) to index terrain data.

Since 0.5 + 0.5 * cos(x) approaches zero at the edges of the "bump", repeatedly applying such modulated terrain fades things together nicely.

Next, craters are optionally added.

Similar to "bumps" except:

Different profile

No terrain sampling

Still needs some work.

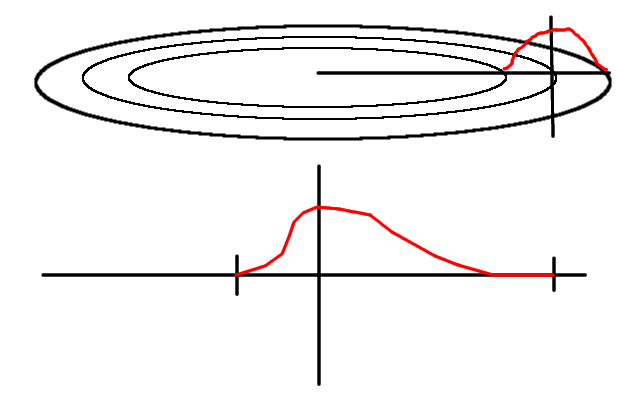
Abusing cosine some more

Next, heightmap data is painted into 6 temporary images

Height is scaled into the range 0 - 255, and RGB channels are set to height. This produces grayscale images where intensity is proportional to altitude.

From the heightmap, normal map images can be calculated.

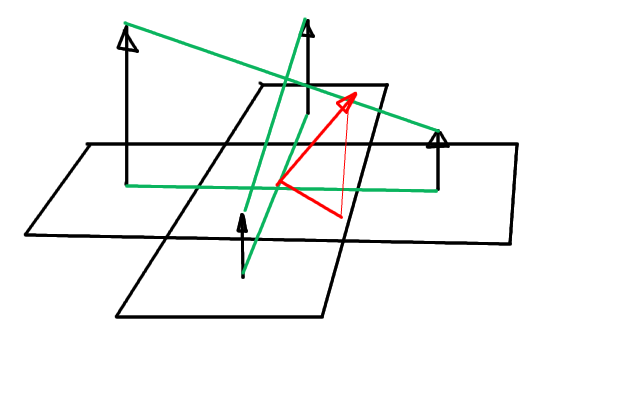
From adjacent pixels, (brightness == height) calculate dh/dx and dh/dy.

From dh/dx and dh/dy, calculate the normal vector:

        x = dh/dx / 127.0f + 0.5;
        y = dh/dy / 127.0f + 0.5;
        z = 1.0f;

Note: if you want oceans, just check height against an arbitrarily chosen "sea level" and if below sea level, the normal is simply set to be straight out from the center of the planet.

Convert normal vectors into images

Encode each vector's x,y,z component into a pixel's red, green, and blue channels, respectively

	red = normal.x * 255;
	green = normal.y * 255;
	blue = normal.z * 255;

Next, real image colors need to be computed.

Simply mapping altitude to colors directly is unsatisfactory

For each vertex, an fBm noise value is calculated

Using altitude for one axis, and this fBm noise value for the 2nd axis, we can index into 2D source images for land and water for above and below sea-level cases, respectively.

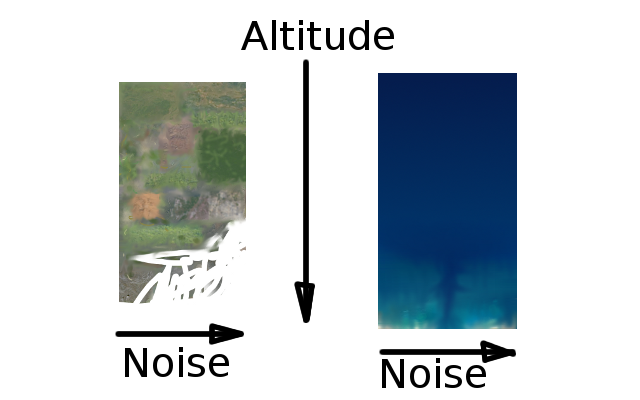
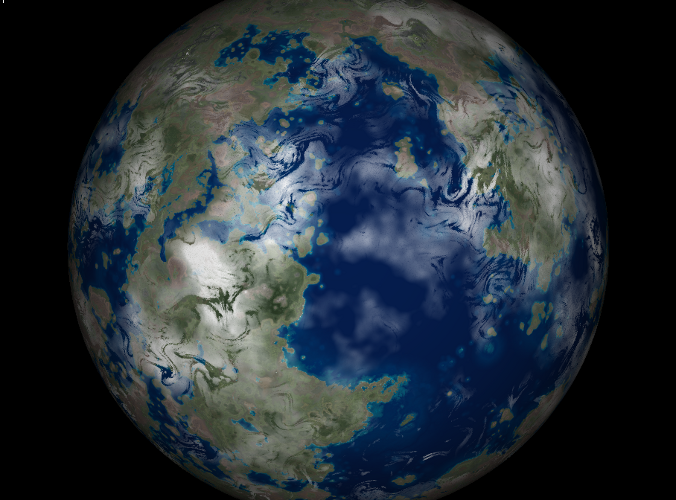
This gets us something like this:

What about clouds?

Clouds are hard

fBm noise, simplex noise, Perlin noise by themselves are not satisfactory

Need to look into Worley noise

How to generate something like what is below? I have no good idea.

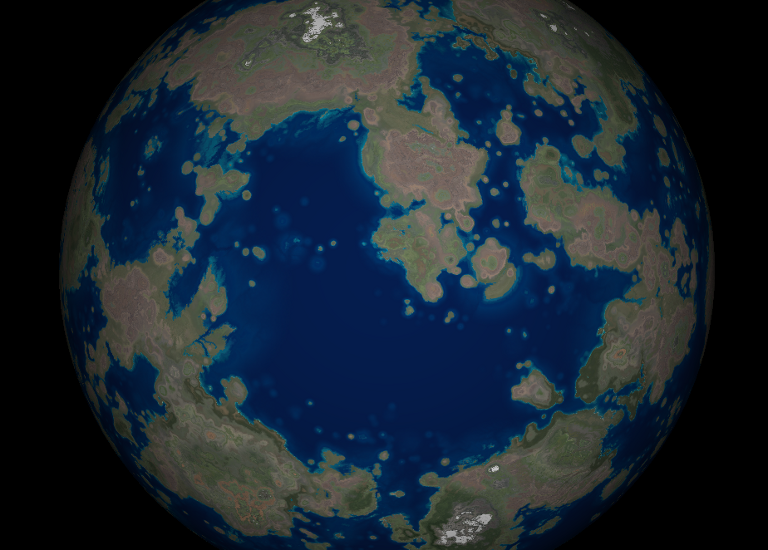
Composite cloud images with terrain images, et voila!

Using no sea-level, craters, and different terrain sample images, we can make moon-like planets:

Some craters...

Links:

• https://github.com/smcameron/space-nerds-in-space